Minitab Statistical Software是一款无与伦比的可视化统计分析软件,它会审视当前及过往的数据,以找出趋势并预测规律、发现变量之间隐藏的关系、可视化数据交互作用并识别重要因素,从而解答最棘手的问题、应对最严峻的难题。
本文将会介绍一些Minitab统计规程中的一些最常见的错误,这些错误涉及从分析结果中得出错误的结论。
统计错误1:错误解释重叠的置信区间
在比较多个均值时,有时建议统计从业人员比较置信区间的结果并确定区间是否重叠。如果两个独立总体的均值的95%置信区间不重叠,则均值之间确实存在统计学上的显着差异(显着性水平为0.05)。但是,情况不一定 相反。 CI可能会重叠,但均值之间可能存在统计上的显着差异。
举个例子:
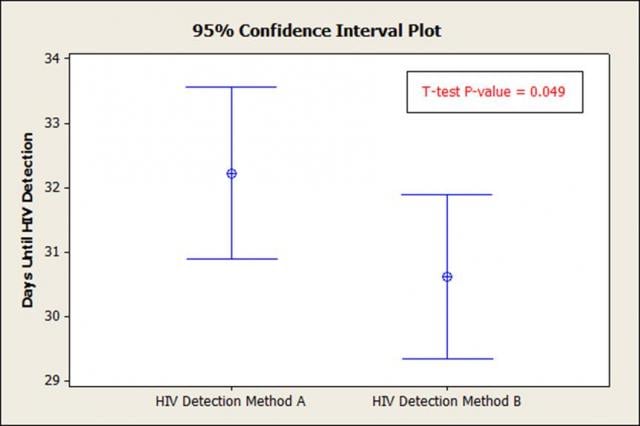
两个重叠的95%置信区间在95%置信度水平上可能会显着不同。
t检验P值的意义是什么?在这种情况下,P值小于0.05(0.049 <0.05),这告诉我们平均值之间存在统计差异(但CI的重叠程度很大)。
统计错误2:对人口做出错误的推断
利用统计数据,我们可以分析一个小的样本来推断整个人口。但是在某些情况下,您应该避免对样本不代表的总体进行推断:
- 在能力分析中,有时会不恰当地使用一天的数据来估计整个制造过程的能力。
- 在验收抽样中,从批次的一部分中选择样本进行整个分析。
- 当可靠性分析中仅包含失败的单元,而总体是生产的所有单元时,就会发生常见且严重的情况。
为避免这些情况,请在采样前定义总体,并采取能真正代表总体的样本。
统计错误3:假设相关=因果关系
它有时会被过度使用,但是在处理统计信息时,“相关性并不意味着因果关系”是一个很好的提醒。两个变量之间的关联并不意味着一个变量会引起另一个变量的变化,特别是如果关联统计是您在数据分析中使用的唯一统计时。
例如,数据分析显示衬衫尺寸和鞋子尺寸之间有很强的正相关性。随着衬衫尺寸的增加,鞋子的尺寸也随之增加。这是否意味着穿大衬衫会使您穿大鞋子?当然不是!这里可能还有其他“隐藏”因素在起作用,例如身高。 (高个子的人倾向于穿更大的衣服和鞋子。)
查看此散点图,该散点图显示HIV抗体假阴性率与患者年龄相关:
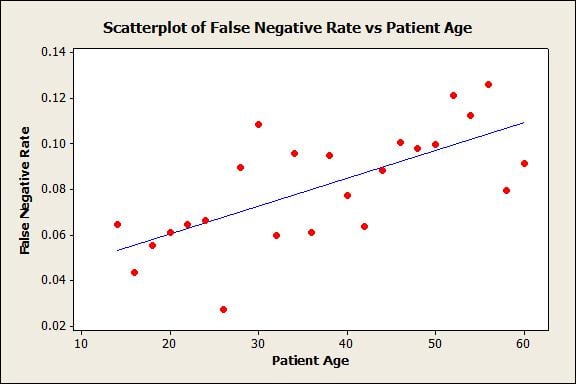
这是否表明HIV抗体测试不适用于老年患者?也许会 …
但是,您不能止步于此,并假设仅仅因为患者年龄较大,才是导致他们获得假阴性测试结果的因素(假阴性是指患者在测试中测试为阴性,但被确认具有这种病)。
让我们深入一点。在下面,您可以看到患者的年龄和有风险的暴露与测试之间经过的天数是相关的:
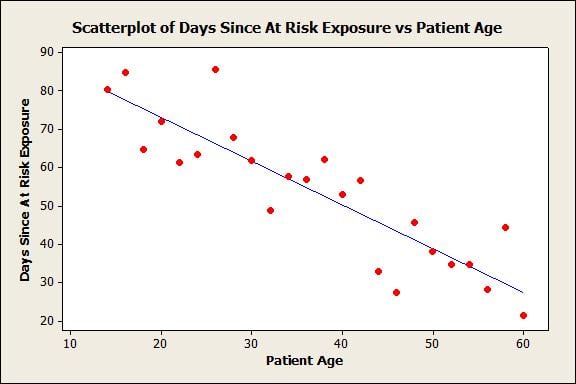
老年患者的检测速度更快……在HIV抗体能够完全发育并显示出阳性检测结果之前。
阅读媒体上公布的许多研究中的某些内容时,请牢记“相关性并不意味着因果关系”的想法。不论有意还是无意,媒体经常暗示一项研究已经揭示了某种因果关系,即使该研究的作者精确地详述了他们研究的局限性。
统计错误4:无法区分统计意义和实际意义
重要的是要记住,使用统计数据,我们可以发现统计上的显着差异,在“现实世界”中没有明显的影响。换句话说,仅仅因为存在差异并不意味着差异重要。而且您可能会浪费大量时间和金钱来尝试“校正”无统计学意义的重大差异。
假设您喜欢Tastee-O的谷物。制造工厂的他们使用自动测量系统在灌装线的末端称重每个谷物盒。假设每个班次装满18,000箱,目标装填重量为360克,标准偏差为2.5克。
使用统计数据,工厂可以在90%的时间内检测到0.06克的平均填充重量偏移。但是,仅因为0.06克偏移具有统计意义,并不意味着它具有实际意义。 0.06克的差异可能相当于两到三个Tastee-O,不足以吸引您,客户,注意或关心。
在大多数假设检验中,我们知道原假设并不完全正确。在这种情况下,我们不希望平均填充重量精确地为360克-我们只是在尝试查看是否存在有意义的差异。代替假设检验,谷物制造商可以使用置信区间来查看差异可能有多大,并决定是否需要采取措施。
统计错误5:说明您已经证明了零假设
在假设检验中,您将构成原假设(H0)和替代假设(H1)。然后,您可以收集数据,对其进行分析,并使用统计信息来评估数据是否支持替代假设。如果p值大于0.05,则表示“没有足够的证据可以得出H5为0.05 /显着性水平”。
换句话说,即使我们没有足够的证据支持替代假设,原假设也可能是正确的,也可能不是。
例如,可以掷3次公平硬币并进行测试:

H0:正面比例= 0.40
H1:正面比例≠0.40
在这种情况下,保证p值大于0.05。因此,不能得出H1。但是不能得出H1并不能证明H0是正确或正确的!这就是为什么说“未能拒绝”原假设,而不是“接受”原假设的原因。
Minitab是做质量分析的工具,不知道您是否有产品质量这方面的困扰呢?不妨试试产品质量分析及预测方案吧!点击咨询在线客服
 023-68661681
023-68661681
 返回
返回






发表评论